11月20日下午,公司党委书记、董事长杨林在公司副总经理、安全监察局局长林青的陪同下到欧宝煤矿调研指导工...
10月23日上午,公司党委书记、董事长杨林深入到任楼矿储煤场、欧宝芬雷任楼选煤厂调研督导煤质、洗选、销售...
10月7日,中秋、国庆节后第一天下午,安徽省皖北煤电集团有限责任公司党委书记、董事长、总经理,公司党委书...
根据中国证监会、上海证券交易所关于披露半年度报告等事项的相关要求,公司于8月16日在总部...
7月21日下午,公司党委书记、董事长杨林到恒泰公司调研指导工作,公司总经理焦殿志陪同调研。 ...
22
2023-11
11月20日下午,公司党委书记、董事长杨林在公司副总经理、安全监察局局长林青的陪同下到欧宝煤矿调研指导工作。 ...
17
2023-11
任楼煤矿 “报告调度,职工宿舍1号楼314房间发生火灾事故。” “立即停掉1#楼供电,立即撤离宿舍员工。” ...
24
2023-10
10月23日上午,公司党委书记、董事长杨林深入到任楼矿储煤场、欧宝芬雷任楼选煤厂调研督导煤质、洗选、销售、精煤任务完成等情况。 ...
09
2023-10
10月7日,中秋、国庆节后第一天下午,安徽省皖北煤电集团有限责任公司党委书记、董事长、总经理,公司党委书记、董事长杨林到祁东矿调研指导...
26
2023-09
9月26日上午8:58分,随着综掘机的轰鸣声,钱营孜煤矿重点接替工程E3212风巷联巷与E3213机巷实现零误差安全贯通,为下一步矿井...
15
2023-09
9月11日,任楼矿重点接替工程——7264工作面实现精准贯通。该矿综掘二区200多名“勇士”大力弘扬“三个不相信”精神,齐心协力,敢啃...
20
2023-11
砥砺奋进三十载,建功“煤”好新时代 ——煤炭工业安全高效煤矿建设30周年暨高质量发展推进会召开 为全面贯彻党的...
21
2023-11
秋去冬来。步入四季度,随着全国气温普遍逐渐走低,各地储备过冬物资正进行得如火如荼,尤其是电煤运输需求大幅增长。煤炭作为供暖取热的主要能...
03
2023-07
全国煤矿智能化建设典型案例汇编(2023年)...
25
2023-06
近日,由国家能源集团数智科技公司承建的煤矿人员定位系统项目顺利通过验收,集团下属56家井工生产矿井全部完成人员定位系统升级改造,构建起...
14
2023-06
煤炭企业全力推动主题教育走深走实 作者:中国煤炭报 本报讯 连日来,广大煤炭企业在开展学习贯彻习近平新时代中国...
06
2023-06
5月31日,国务院安委会办公室、应急管理部在京举行全国“安全生产月”活动启动仪式。中共中央政治局委员、国务院副总理张国清出席并宣布20...
17
2023-11
31
2023-10
近年来,钱营孜矿坚持以员工为中心,时刻把职工所思所想所盼放在心上,坚持把好事办好、实事办实,让民生举措更有“温度”、惠民答卷更有“厚度...
18
2023-08
16
2023-08
21
2023-07
强国品牌,辉耀京华。7月15日,由专业品牌评价机构Asiabrand发起主办,中国亚洲经济发展协会、环球时报社、中国经济新闻联播网等机...
14
2023-07
14
2023-10
上证发〔2023〕157号 各市场参与人: 为加强融券逆周期调节,维护证券市场交易秩序,经中国证监会批准,上海...
13
2023-09
中共中央、国务院关于加快建设全国统一大市场的意见 (2022年3月25日) 建设全国统一大市场是构建新发展格局...
13
2023-09
...
09
2023-08
上海证券交易所上市规则(2023年8月)...
09
2023-08
上海证券交易所上市公司自律监管指引第1号——规范运作(2023年8月)...
07
2023-08
上市公司独立董事管理办法(2023年8月)...



见证企业实力 打造优良品牌



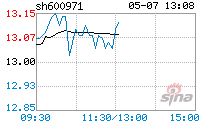
欧宝游戏平台由安徽省皖北煤电集团有限责任公司作为主发起人,于2000年12月29日发起设立,主要从事煤炭开采、洗选加工、销售等业务,在岗员工一万四千多人。2004年8月,公司首次成功向社会公开发行A 股股票4,400万股,并在上海证券交易所上市交易,成为安徽省上市的煤炭企业。公司股票简称“欧宝游戏平台”,股票代码600971。
公司地处经济发达的华东地区,坐落在全国13个亿吨级煤炭基地之一的两淮基地,目前下辖5对矿井、5座配套选煤厂。公司煤种齐全,主要有贫瘦煤、1/3焦煤、气肥煤、无烟煤、主焦煤等;煤炭产品主要有混煤、洗末煤、冶炼精煤等,核定年生产能力1095万吨;煤炭质量优良,低硫、低磷、低灰、高发热量,有“绿色环保”能源的美称,广泛应用于电力、冶金、石化、建材、炼焦、高炉喷吹、民用等领域,是理想的动力用煤和生活用煤......




